質量を
 、力を
、力を  としたとき、物体の加速度の大きさは
としたとき、物体の加速度の大きさは  に比例し、その物体の質量に反比例する。 式で表すと
に比例し、その物体の質量に反比例する。 式で表すと 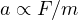 となる。この式の係数を1として、
となる。この式の係数を1として、
1.4 運動の法則
物体は運動状態を保持しようという性質をもつ、この性質を慣性いう。また慣性の大きさを表す量を質量と表す。
ニュートンの第一法則(慣性の法則)
物体に他から何の作用もなければ、物体は静止しつづけるか、速さが一定な運動を続ける。
例えば、力などの作用がない限り、机の上におかれた物体は、いくら時間が経っても動き出すことはないし、宇宙空間を進んでいるロケットは隕石などと衝突しない限り、進み続ける。
ニュートンの第二法則(運動の法則)
質量を  、力を
、力を  としたとき、物体の加速度の大きさは
としたとき、物体の加速度の大きさは  に比例し、その物体の質量に反比例する。 式で表すと
に比例し、その物体の質量に反比例する。 式で表すと 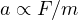 となる。この式の係数を1として、
となる。この式の係数を1として、

「質量 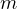 」 × 「加速度
」 × 「加速度  」= 「力
」= 「力  」 が成り立つことをニュートンが発見した。
例えば、物体を手で押して動かすときに、軽い(質量が小さい)と直ぐ動き出すが、軽いときに比べて重い(質量が大きい)と動かせてもゆっくりと動き出すことから、質量、加速度、力の関係は生活の中で実感できる。
」 が成り立つことをニュートンが発見した。
例えば、物体を手で押して動かすときに、軽い(質量が小さい)と直ぐ動き出すが、軽いときに比べて重い(質量が大きい)と動かせてもゆっくりと動き出すことから、質量、加速度、力の関係は生活の中で実感できる。
ニュートンの第三法則(作用 ⋅反作用の法則)
2 個の物体 1、2 を衝突させると、物体 1 に加わる 2 からの力  、物体 2 に加わる 1 からの力
、物体 2 に加わる 1 からの力 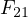 は下記のように向きが逆で、方向、大きさが等しい。
は下記のように向きが逆で、方向、大きさが等しい。


例えば、作用 ⋅反作用の法則は、氷の上で相手を手で押すと自分も反対方向へ動くことからも実感できる。
質量:物体の運動の変化のしにくさの程度を表す量。単位: kg
当初、1 kg は 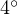 C の水 1
C の水 1  の質量として定義され、近年まで国際度量衡局(フランス・パリ)にあるキログラム原器の質量によって定義されていた。 現在は、プランク定数
の質量として定義され、近年まで国際度量衡局(フランス・パリ)にあるキログラム原器の質量によって定義されていた。 現在は、プランク定数
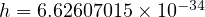 (J ⋅ s) を使ってエネルギーで定義(
(J ⋅ s) を使ってエネルギーで定義( 、(
、(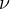 、読みニュー、振動数))されている。
、読みニュー、振動数))されている。
1.5 単位系
SI (単位系) : 長さm(メートル)「1 m は光が真空中で1秒間に進む距離の 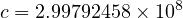 (m/s)(真空中の光速)分の 1 の長さと定義」、質量 kg(キログラム)「1
kg は(
(m/s)(真空中の光速)分の 1 の長さと定義」、質量 kg(キログラム)「1
kg は(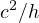 )Hz の周波数を持つ光子のエネルギー(テキストp.309 参照)に等価な質量と定義、1 [kg] =
)Hz の周波数を持つ光子のエネルギー(テキストp.309 参照)に等価な質量と定義、1 [kg] = 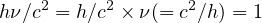 、
、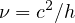 の振動数を持つ光子のエネルギーと等しい」、時間s(秒)「1 秒はセシウム 133原子(133Cs)の基底状態の2つの超微細構造準位の間の遷移に対応した放射する特定の電磁波が 9192631770
回振動する時間を 1 秒と定義」
の振動数を持つ光子のエネルギーと等しい」、時間s(秒)「1 秒はセシウム 133原子(133Cs)の基底状態の2つの超微細構造準位の間の遷移に対応した放射する特定の電磁波が 9192631770
回振動する時間を 1 秒と定義」
力の単位は 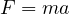 、 1 kg × 1 m/s2= 1 N (ニュートン)と呼ぶ。1.0 kg の質量にかかる重力は
、 1 kg × 1 m/s2= 1 N (ニュートン)と呼ぶ。1.0 kg の質量にかかる重力は

と表される。
力(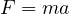 )の次元(組み合わせ単位の形)は [MLT-2] である。 ここで、M は質量(mass)、L は長さ(length)、T は時間(time)を表す。 質量
)の次元(組み合わせ単位の形)は [MLT-2] である。 ここで、M は質量(mass)、L は長さ(length)、T は時間(time)を表す。 質量 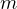 の次元は
[M]、速度
の次元は
[M]、速度 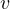 の次元は
の次元は 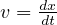 (距離 / 時間)から [L/T]、加速度
(距離 / 時間)から [L/T]、加速度  の次元は
の次元は 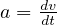 (速度 / 時間)から [(L/T)/T] となり、力の次元は [MLT-2]
となる。 求めた式が正しいかどうか分からないときに、両辺の次元が同じかどうかの確認を行い、式が正しいかどうかを確かめることができる。
(速度 / 時間)から [(L/T)/T] となり、力の次元は [MLT-2]
となる。 求めた式が正しいかどうか分からないときに、両辺の次元が同じかどうかの確認を行い、式が正しいかどうかを確かめることができる。
<例題6>
5.0 kg のブロックがなめらかな床に置かれており、これに糸で連結された 4.0 kg の物体が滑車を通して吊るされている。糸と滑車には重さはないとき、物体が落下する加速度  と糸の張力
と糸の張力 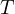 を求めよ。
を求めよ。
5.0 kg のブロックを 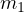 、4.0 kg のブロックを
、4.0 kg のブロックを  として、図のようにブロックに働く全ての力が記入されている。 ここでは必要がないが、
として、図のようにブロックに働く全ての力が記入されている。 ここでは必要がないが、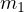 に働く重力(
に働く重力( )と床から
)と床から  に働く垂直抗力
に働く垂直抗力 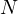 も記入されている。なぜなら、
も記入されている。なぜなら、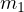 は床があるので垂直方向へは動かない(このことは
は床があるので垂直方向へは動かない(このことは  に働く垂直方向の力がゼロ(
に働く垂直方向の力がゼロ(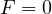 )であることを示す)ので、考慮しなくて良い。 ただし、垂直方向の力のつり合いの関係式(
)であることを示す)ので、考慮しなくて良い。 ただし、垂直方向の力のつり合いの関係式(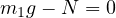 )から、
)から、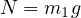 となる。
となる。

質量  のブロックは糸によって張力
のブロックは糸によって張力 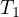 で引っ張られ、質量
で引っ張られ、質量  の物体は糸によって張力
の物体は糸によって張力 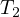 で引っ張られている。作用 ⋅反作用の法則から
で引っ張られている。作用 ⋅反作用の法則から 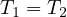 である。よって、運動方程式(
である。よって、運動方程式( )は
)は 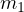 と
と 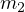 の加速度を
の加速度を 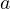 (糸で繋がっているので、動く距離は同じ、すると加速度も同じ大きさ)として
(糸で繋がっているので、動く距離は同じ、すると加速度も同じ大きさ)として
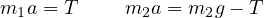
となる。ここで 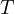 は力
は力 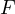 の代わりであり、
の代わりであり、 の落下する方向を正(+)にとった。 両式の和(右辺と左辺の和、
の落下する方向を正(+)にとった。 両式の和(右辺と左辺の和、 を消去)を作ると、以下のようになる。
を消去)を作ると、以下のようになる。
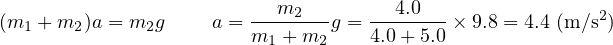
これを上式( )に代入して、
)に代入して、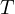 を求める。
を求める。
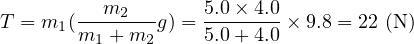
計算に使用した値の有効数字は2桁の 5.0 kg、4.0 kg、9.8 m/s2であり、そのため、求める解も2桁(4.4 m/s2、22 N)で回答しなけらばならない。(下記の例題7も同様に回答しなければならない)
<例題7>
質量 4.0 kg (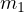 )と 5.0 kg (
)と 5.0 kg (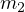 )の 2 のブロックをなめらかな床の上に置き、糸で連結しておく。5.0 kg のブロックの方を 10 N (
)の 2 のブロックをなめらかな床の上に置き、糸で連結しておく。5.0 kg のブロックの方を 10 N ( )で引っ張るとき、糸の張力
)で引っ張るとき、糸の張力 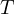 はいくらか。また、それぞれの加速度
はいくらか。また、それぞれの加速度 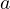 はいくらか。
はいくらか。
糸の張力の大きさを  (
(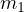 と
と  に作用する張力は作用反作用のために同じ)、
に作用する張力は作用反作用のために同じ)、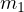 = 4.0 kg、
= 4.0 kg、 = 5.0 kg、
= 5.0 kg、 = 10 N
として、運動方程式(
= 10 N
として、運動方程式(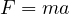 )は
)は
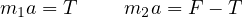
と得られる。 下記のように、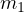 と
と  が一体となって
が一体となって 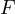 に引っ張られるときの加速度と同じである。 垂直方向については、例題6と同様に垂直抗力
に引っ張られるときの加速度と同じである。 垂直方向については、例題6と同様に垂直抗力  、
、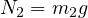 となる。
となる。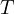 を消去して
を消去して

と計算される。これを 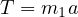 に代入して、
に代入して、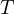 を求める。
を求める。


1.6 万有引力
すべての物体は、2 つの物体の質量(それぞれの質量を  、
、 とする)の積に比例し、その間の距離
とする)の積に比例し、その間の距離  の二乗
の二乗  に反比例する力で引き合っている。これを万有引力の法則といい、式で表わすと
に反比例する力で引き合っている。これを万有引力の法則といい、式で表わすと

となる。(負符号が付いている場合は引力を示す。)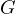 は万有引力定数 (
は万有引力定数 ( 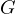 = 6.674 × 10-11 N ⋅ m2 / kg2 ) である。
= 6.674 × 10-11 N ⋅ m2 / kg2 ) である。

なお地球の半径を 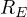 ,質量を
,質量を 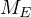 とすると、地球上にある
とすると、地球上にある  (kg) の物体に働く引力は
(kg) の物体に働く引力は
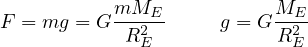
と表わされ、万有引力定数と重力加速度 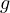 の間の関係を示している。 この式は単に地球の質量が中心に集まり、中心からの距離
の間の関係を示している。 この式は単に地球の質量が中心に集まり、中心からの距離 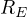 離れた質量
離れた質量 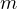 に働く万有引力を示す。
に働く万有引力を示す。
ただし、南極と北極における  の値が最も大きく、赤道における
の値が最も大きく、赤道における 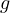 の値が最も小さい。これは地球の自転による遠心力の影響ために生じ、緯度によって変化する。また、その方向も地球の中心からずれる。
の値が最も小さい。これは地球の自転による遠心力の影響ために生じ、緯度によって変化する。また、その方向も地球の中心からずれる。

1.7 力と運動
一般に物体の運動は微分方程式で記述される。これら微分方程式を解いて初めて、物体の運動の様子が分かる。
<例題 8> (テキストp.43 参照)
質量 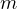 の物体を初速
の物体を初速  、仰角(角度 θ )で投げるときの運動を求めよ。(21 ページ<例題4>の異なった考え方である。)
、仰角(角度 θ )で投げるときの運動を求めよ。(21 ページ<例題4>の異なった考え方である。)
物体に作用する 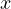 、
、 、
、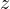 方向の加速度を使って記述される運動方程式(
方向の加速度を使って記述される運動方程式(  、数学的には微分方程式)を積分することによって、運動の様子(軌道)を求める。
空中で物体に働く力はz軸方向の重力加速度
、数学的には微分方程式)を積分することによって、運動の様子(軌道)を求める。
空中で物体に働く力はz軸方向の重力加速度 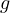 による力
による力 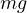 のみであり、
のみであり、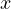 と
と 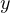 軸方向には力は働かない。 よって、
軸方向には力は働かない。 よって、 、
、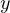 、
、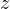 軸方向の運動方程式は
軸方向の運動方程式は

と書くことができる。これを 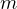 で両辺を割って
で両辺を割って  、
、 、
、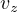 を使って書き直すと
を使って書き直すと
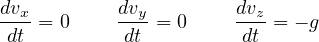
となる。これらの式の両辺に 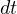 を掛けて、積分(∫
を両辺に書く)すると
を掛けて、積分(∫
を両辺に書く)すると

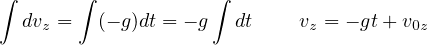
と計算される。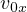 、
、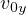 、
、 は積分定数である。 確認するには微分してみると良い。 次に、
は積分定数である。 確認するには微分してみると良い。 次に、 、
、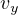 、
、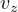 を
を  、
、 、
、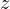 を使って書くと
を使って書くと
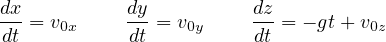
となる。これらの式に 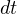 を両辺に掛けて、式を積分(∫
を両辺に書く)すると
を両辺に掛けて、式を積分(∫
を両辺に書く)すると
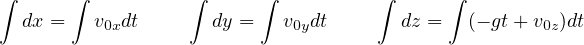
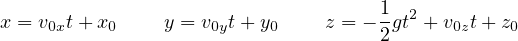
と積分される。 初期条件として 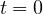 のとき
のとき 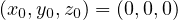 かつ
かつ 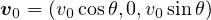 (原点から投げる、かつ 各軸方向の初速度成分が
(原点から投げる、かつ 各軸方向の初速度成分が
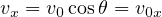 、
、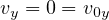 、
、 )であることを考慮すると
)であることを考慮すると
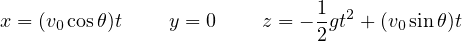
となる。 当然、積分することによって得られた 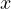 、
、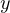 、
、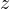 を微分すると、
を微分すると、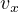 、
、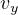 、
、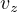 を求めることができ、正しいことが確認できる。つまり、初期条件を満たすように、積分定数など決定する。
次に、上式の
を求めることができ、正しいことが確認できる。つまり、初期条件を満たすように、積分定数など決定する。
次に、上式の 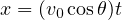 を使って、
を使って、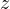 式の
式の  を消去すると
を消去すると
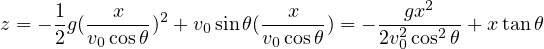
となり、この式は物体の運動の位置  を与える。 つまり、
を与える。 つまり、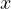 が指定されると、
が指定されると、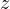 の位置が決定される。 物体は放物線上を運動する。落下点は
の位置が決定される。 物体は放物線上を運動する。落下点は 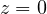 から
から

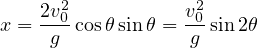
となり、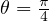 (rad、ラジアン)(
(rad、ラジアン)(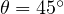 )のとき
)のとき 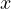 が最大距離を示す。 なお、
が最大距離を示す。 なお、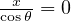 ( cosθ は 0 でないので、
( cosθ は 0 でないので、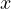 = 0 である)の点は原点を示す。
三角関数の変形は2倍角の公式 sin2θ = 2sinθ cosθ を用いた(例題4参照)。
= 0 である)の点は原点を示す。
三角関数の変形は2倍角の公式 sin2θ = 2sinθ cosθ を用いた(例題4参照)。
