 の物体が速度
の物体が速度 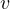 で運動しているとき、物体がもつ運動エネルギーは
で運動しているとき、物体がもつ運動エネルギーは  であった。 いま、質量
であった。 いま、質量 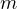 の物体が床より
の物体が床より  の位置にある。初速度
の位置にある。初速度 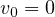 で床に落ちたとき、物体が持つエネルギーはどうなるか。
で床に落ちたとき、物体が持つエネルギーはどうなるか。
1.19 エネルギー保存則
質量  の物体が速度
の物体が速度 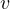 で運動しているとき、物体がもつ運動エネルギーは
で運動しているとき、物体がもつ運動エネルギーは  であった。 いま、質量
であった。 いま、質量 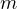 の物体が床より
の物体が床より  の位置にある。初速度
の位置にある。初速度 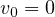 で床に落ちたとき、物体が持つエネルギーはどうなるか。
で床に落ちたとき、物体が持つエネルギーはどうなるか。
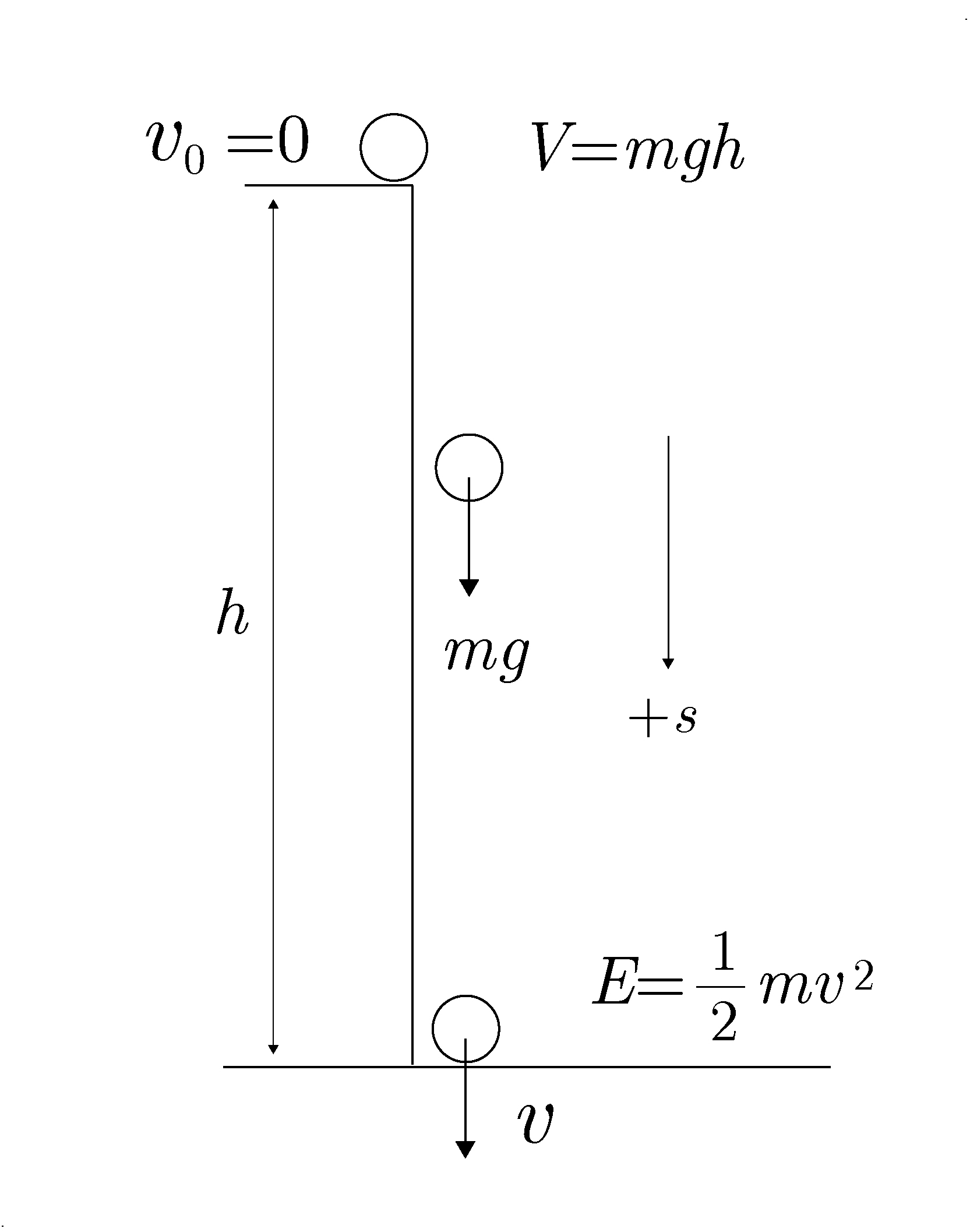
物体の運動は
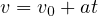
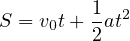
によって記述される。  の式から
の式から 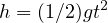 になるので、床に到達する時間
になるので、床に到達する時間  は
は
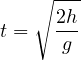
と得られる。 床に着く直前の 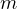 の速さは上式の
の速さは上式の 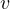 に
に  を代入して
を代入して
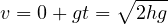
となる。よって、運動エネルギー  は
は
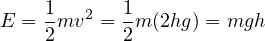
となり、位置エネルギー 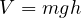 と同じである。つまり位置エネルギーが運動エネルギーに変わったことになる。エネルギーが不変な量であることをエネルギー保存則という。
と同じである。つまり位置エネルギーが運動エネルギーに変わったことになる。エネルギーが不変な量であることをエネルギー保存則という。
1.20 仕事率
単位時間(1 秒間)あたりエネルギーが放出される割合を仕事率(パワー)という。仕事率 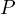 は、仕事をその仕事にかかった時間で割って
は、仕事をその仕事にかかった時間で割って
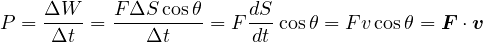
で定義される。つまり、単位時間(1 秒)あたりの仕事の量である。 仕事率の単位は [W](ワット、1 [W] = 1 [J/s])で表される。 例えば、30 [W] の蛍光灯は
1 秒間に 30 [J] のエネルギーを消費する。 1 時間の間、蛍光灯を使ったとすると 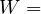 30
30  60 (s)
60 (s) 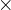 60 (min) = 108 (kJ)
のエネルギーが消費される。つまり、消費されるエネルギーを求めるには仕事率に使用時間を掛けなければならない。 家で必要とされるエネルギー(電力など)は、色々な機器の単位時間(1
秒間)あたりに消費されるエネルギー(仕事率)の合計から求められ、契約電力などが決定される。
60 (min) = 108 (kJ)
のエネルギーが消費される。つまり、消費されるエネルギーを求めるには仕事率に使用時間を掛けなければならない。 家で必要とされるエネルギー(電力など)は、色々な機器の単位時間(1
秒間)あたりに消費されるエネルギー(仕事率)の合計から求められ、契約電力などが決定される。
1.21 運動方程式の積分
物体の質量 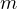 と速度
と速度 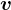 の積を運動量 (
の積を運動量 (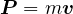 )という。運動量は保存量(不変なもの、時間的に変わらないもの)であり、勝手に増えたり減ったりしない。
この運動量を用いて、ニュートンの運動方程式を記述すると
)という。運動量は保存量(不変なもの、時間的に変わらないもの)であり、勝手に増えたり減ったりしない。
この運動量を用いて、ニュートンの運動方程式を記述すると
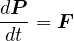
と書ける。両辺に 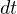 を掛けて積分記号を付け、
を掛けて積分記号を付け、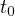 から
から  まで積分すると
まで積分すると
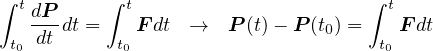
となる。 運動量の時間変化(左辺)は物体に作用する力(これを力積という)に等しい。また、右辺は
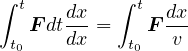
に変形できる。
次に、一次元の運動方程式(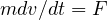 )の両辺に
)の両辺に 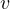 と
と 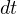 を掛けて
を掛けて 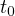 から
から  まで積分すると
まで積分すると
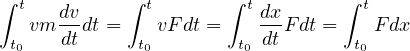
となる。左辺は
![∫ t ∫ t 2
vm dv dt = mvdv = [mv-]tt0 = 1mv2 (t)- 1 mv2(t0)
t0 dt t0 2 2 2](8text39x.png)
となる。よって
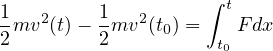
左辺の運動エネルギーの変化量(増加)はなされた仕事(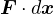 )の合計に等しいことが分かる。 運動方程式の積分から、運動量の変化が力積に等しいこと、また運動エネルギーの変化量がなされた仕事に等しいことが得られる。
)の合計に等しいことが分かる。 運動方程式の積分から、運動量の変化が力積に等しいこと、また運動エネルギーの変化量がなされた仕事に等しいことが得られる。
1.22 保存力
力がある位置の関数 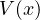 の微分の形で表されるとき、このような力を保存力という。これを式で表わすと
の微分の形で表されるとき、このような力を保存力という。これを式で表わすと
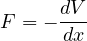
と定義される。 この式の両辺に 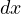 を掛けて
を掛けて 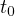 から
から  まで積分すると
まで積分すると
![∫ t ∫ t
Fdx = - dVdx = - [Vt - Vt0]
t0 t0 dx](8text47x.png)
となる。また、上述の運動エネルギーの変化量と仕事の関係式を用いて
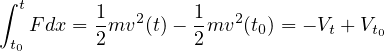
と書くことができる。 同じ時刻になるように整理すると
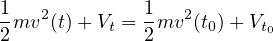
と表わされる。これはある時刻  と
と 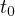 でエネルギーが同じであることを示す。
でエネルギーが同じであることを示す。 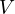 は位置エネルギーである。力がある位置の関数
は位置エネルギーである。力がある位置の関数 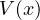 の微分の形で表される系(保存場、下記参照)ではエネルギー保存則が成り立つ。
の微分の形で表される系(保存場、下記参照)ではエネルギー保存則が成り立つ。
ここで、3次元に拡張すると
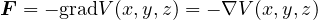
と定義される。ただし、

である。  は演算子(読み:ナブラ)であり、勾配(gradient)を意味する。
は演算子(読み:ナブラ)であり、勾配(gradient)を意味する。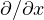 は偏微分(
は偏微分(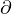 :読み「ラウンド」)を表わし、
:読み「ラウンド」)を表わし、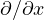 の意味は
の意味は 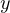 と
と 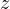 を定数として微分を行うことである。関数
を定数として微分を行うことである。関数 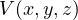 は微分可能でなければならない。
は微分可能でなければならない。
一次元で考察した運動エネルギーを3次元で考察すると、運動方程式(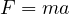 )は
)は
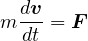
であるので、この両辺に 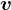 を掛けて内積を作ると
を掛けて内積を作ると
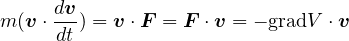
となる。内積の計算において、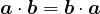 であることを使った。 右辺は
であることを使った。 右辺は
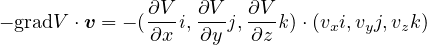
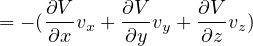
のように変形される。 次に、両辺に  を掛けて、
を掛けて、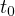 から
から  まで積分すると、左辺は
まで積分すると、左辺は
![∫ ∫
t dv- t 1 2t 1 2 1 2
t0 m (v⋅ dt)dt = t0 mvdv = [2mv ]t0 = 2mv (t)- 2mv (t0)](8text73x.png)
となる。ベクトル 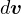 の向きは
の向きは 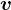 と同じ向き(
と同じ向き(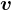 の微小量が
の微小量が 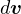 である、
である、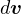 は
は 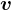 の一部である)であるので、
の一部である)であるので、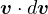 は
は 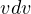 になる。積分すると
になる。積分すると
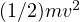 となる。 右辺は
となる。 右辺は
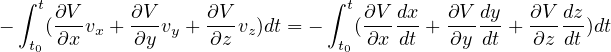
![= - [Vx + Vy +Vz]tt = - [Vt - Vt0]
0](8text84x.png)
と変形できる。 ここで 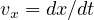 (
(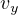 と
と 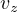 も同じ)の
も同じ)の 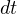 は括弧に掛かっている
は括弧に掛かっている 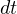 と約分され、
と約分され、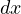 が残る。 次に、
が残る。 次に、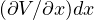 は
は  を
を 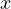 で偏微分し、積分することを意味する。この偏微分を以下に記述(多少無理があるが)すると
で偏微分し、積分することを意味する。この偏微分を以下に記述(多少無理があるが)すると

となる。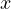 で偏微分すると
で偏微分すると 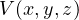 (
(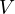 は位置
は位置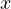 、
、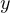 、
、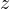 の関数、掛算などで表されていない)中の
の関数、掛算などで表されていない)中の 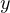 と
と 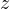 成分がなくなる。 偏微分したあとは
成分がなくなる。 偏微分したあとは 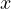 のみの関数となる。 それを
のみの関数となる。 それを 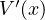 と表し、すると
と表し、すると 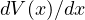 とも書くことができる。
とも書くことができる。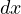 が約分でき、上式のように
が約分でき、上式のように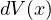 の積分となり、積分すると
の積分となり、積分すると 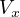 が得られる。
最終的に上式と同様に
が得られる。
最終的に上式と同様に
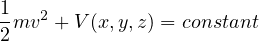
一定(constant)となる。
1.23 保存場
関数 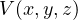 が存在し、力
が存在し、力 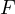 が
が
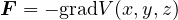
で定義されるとき、この力を保存力、この空間のことを保存場という。 例えば、保存場として、電場、磁場、重力場などが挙げられ、保存力としてクーロン力や万有引力などが挙げられる。
保存場中において保存力によってなされる仕事は始点 A と B のみに依存する。 これは、摩擦や抵抗などがなく、A と B の間のどの様な経路をたどっても良いことを意味する。 このときの仕事
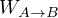 は上式と同様に計算され
は上式と同様に計算され
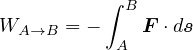
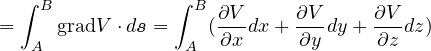
![= [VB - VA]](8text116x.png)
となる。ただし、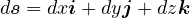 である。 保存場中において閉曲線に沿って移動したとき(一周するとき)、なされた仕事は 0 である。 一周する場合は
である。 保存場中において閉曲線に沿って移動したとき(一周するとき)、なされた仕事は 0 である。 一周する場合は
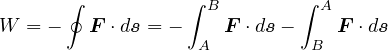
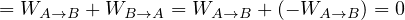
となる。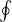 は任意の閉曲線に沿った線積分である。 このとき、微小な領域(図参照)を考え、Fが有しているる条件を以下に示す。以下の微小領域
は任意の閉曲線に沿った線積分である。 このとき、微小な領域(図参照)を考え、Fが有しているる条件を以下に示す。以下の微小領域
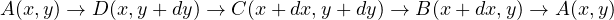
の積分(経路に沿った線積分)を考える。
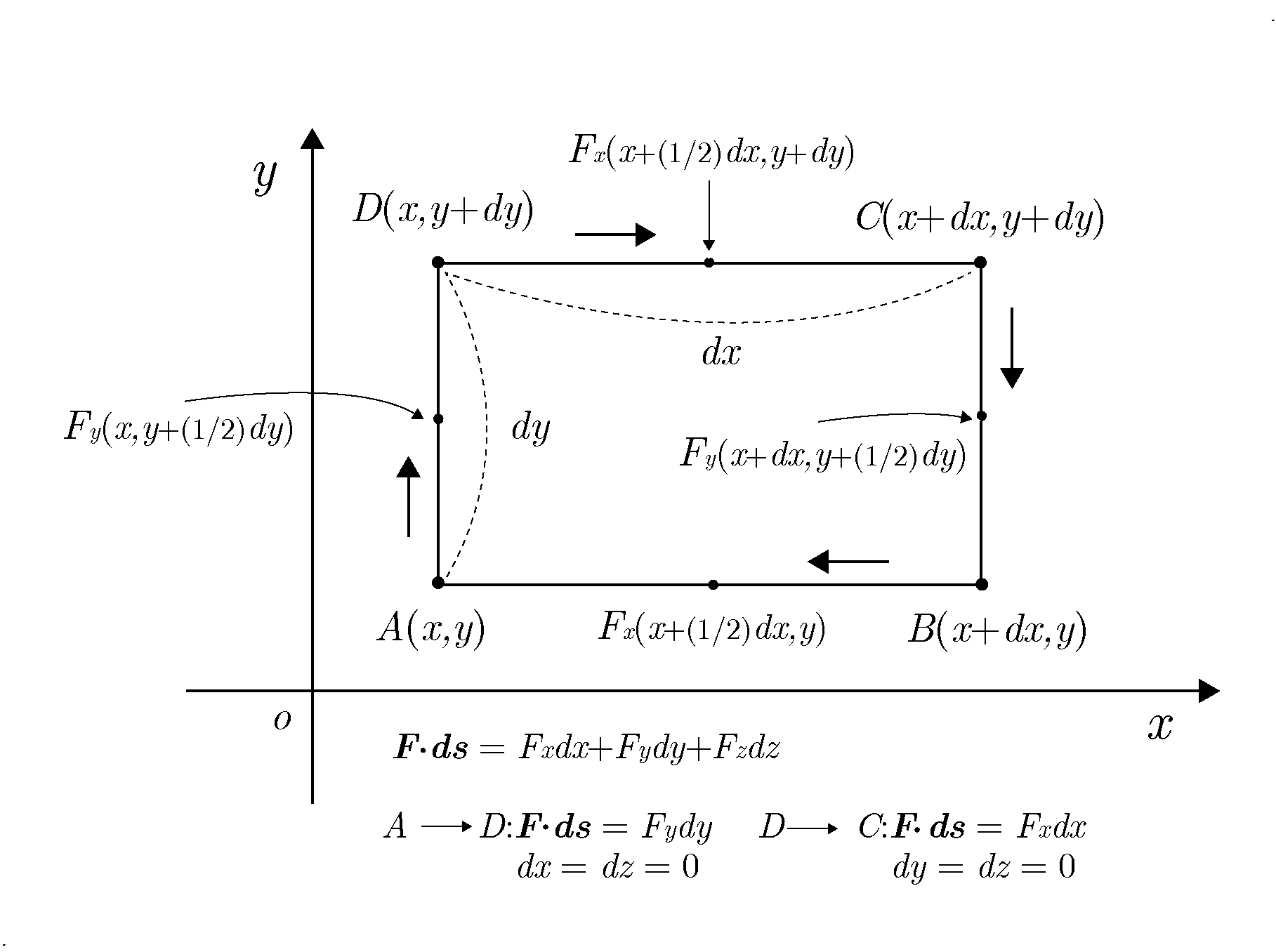
すると
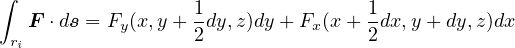

と計算される。ただし、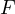 の値として中間の値(例えば、A と D との中間の値など)を用いた。 また、
の値として中間の値(例えば、A と D との中間の値など)を用いた。 また、
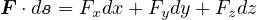
であるで、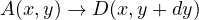 での積分は
での積分は 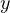 方向へ
方向へ 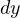 だけが増える(
だけが増える(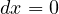 、
、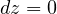 )ので、上式の
)ので、上式の 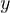 成分
成分  が残り、
が残り、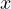 と
と  成分はゼロになる。 整理すると
成分はゼロになる。 整理すると
![1 1
= [Fy (x,y + 2dy,z)- Fy(x+ dx,y+ 2dy,z)]dy](8text135x.png)
![1 1
+[Fx(x+ 2dx,y+ dy,z)- Fx(x+ 2 dx,y,z)]dx](8text136x.png)
となる。 テイラー展開の第1項目

を使って、上式の展開を行う。ただし、この展開の第1項目は微分(傾き)の定義式
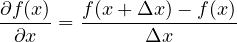
になっていることが分かる。 例えば、
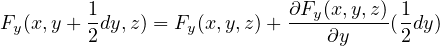
と展開される。 整理された式を展開すると
![∂Fy1 ∂Fy- ∂Fy-1
= [Fy(x,y,z) + ∂y 2 dy- Fy(x,y,z)- ∂x dx - ∂y 2dy]dy](8text140x.png)
![∂Fx-1 ∂Fx- ∂Fx1
+ [Fx (x,y,z)+ ∂x 2dx + ∂y dy - Fx(x,y,z) - ∂x 2 dx]dx](8text141x.png)
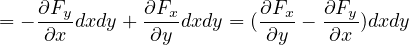
となる。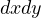 は面積(
は面積(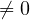 )であり、0 でない。 よって、
)であり、0 でない。 よって、
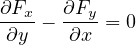
である。これは

で求まるので、これを上式に代入すると
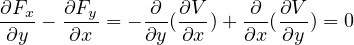
となる。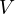 を
を 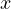 と
と 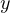 で偏微分するので、偏微分する順番は関係なく当然同じ値になる。 同様に
で偏微分するので、偏微分する順番は関係なく当然同じ値になる。 同様に

となり、これらをまとめると、外積(ベクトル積)で表され
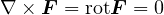
と得ることができる。外積に関しては第1回の講義を参照して下さい。成分で書くと
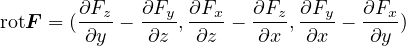
となる。 つまり、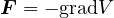 で表される保存力
で表される保存力 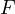 は
は 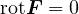 を必ず満たす。最初の積分の式を書くと
を必ず満たす。最初の積分の式を書くと
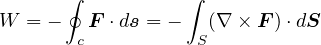
となる。これは線積分と面積分の関係を与える。線積分は閉曲線に沿って1週の積分を行う。右辺の面積分は考えている面全体を積分する。積分中の 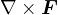 は回転を意味し、線積分から計算されたものでるので、その閉曲線のみに値が存在する。 面積分を行っても枠線上が積分され(枠線以外は何もないので、積分しても0になる)、線積分と同じ値となる(図参照)。
は回転を意味し、線積分から計算されたものでるので、その閉曲線のみに値が存在する。 面積分を行っても枠線上が積分され(枠線以外は何もないので、積分しても0になる)、線積分と同じ値となる(図参照)。
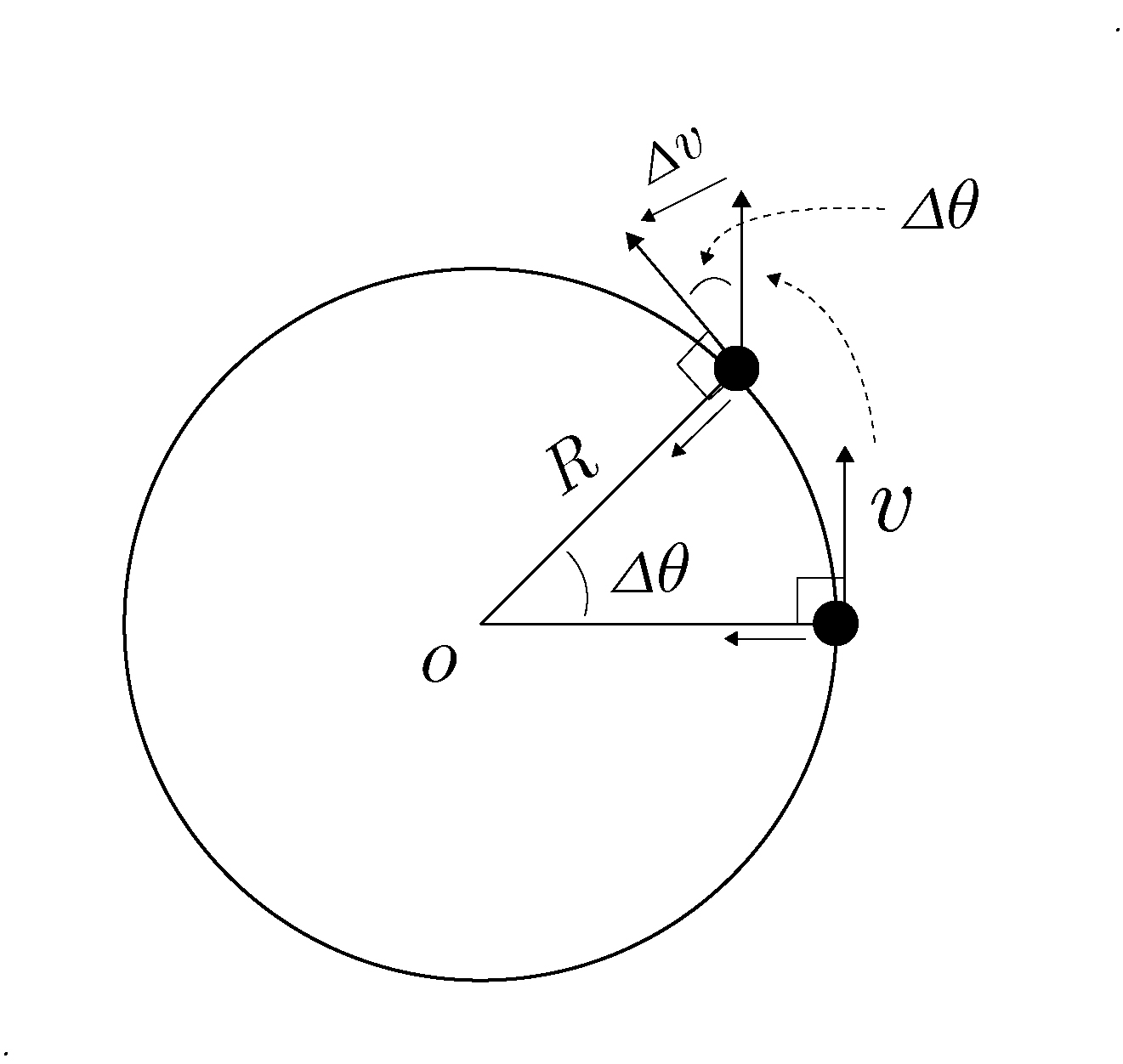
1.24 円運動と遠心力
一定の速さ 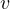 で半径
で半径 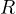 の円運動をしている物体について考える。 座標を極座標に選べば、動径成分(
の円運動をしている物体について考える。 座標を極座標に選べば、動径成分( 方向)
方向) の変化はなく、角度
の変化はなく、角度 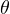 のみが変化する。 図のように、
のみが変化する。 図のように、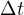 の間に変化する角度は
の間に変化する角度は
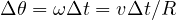
と表される。 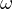 は角速度であり、
は角速度であり、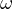 と
と 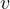 との間の関係
との間の関係 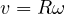 を用いた。 速度の変化分
を用いた。 速度の変化分 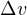 は
は 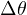 を代入することによって
を代入することによって
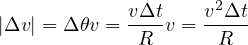
と変形される。例題12 中で記載されたように円周の長さは半径とその間の角度を掛けたものである。 この場合、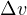 の大きさは
の大きさは 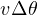 と計算される。 ここで、
と計算される。 ここで、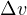 は動径成分の内側を向いているベクトルである。 運動方程式は
は動径成分の内側を向いているベクトルである。 運動方程式は 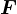 を中心力として
を中心力として
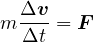
と書ける。これは物体が飛び出さないように中心方向へ引っ張っていることを示す。 例えば、糸におもりを付け回転させた場合、おもりが飛んでいかないように糸がおもり中心方向へ引っ張っている。糸が切れるとおもりはどこかへ飛んで行ってしまうことからも分かる。
また、この式に 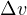 の式を代入すると
の式を代入すると
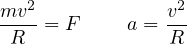
となる。 中心力 F を向心力という。 は動径方向の加速度で、向心加速度という。向心加速度は速さが速いほど、円運動の円の半径が小さいほど大きい。
は動径方向の加速度で、向心加速度という。向心加速度は速さが速いほど、円運動の円の半径が小さいほど大きい。
<例題13>
100 km/h の速さの自動車が、極率半径 150 m のカーブを曲がろうとした。このときの加速度を求めよ。 を時速から秒速に換えると、
を時速から秒速に換えると、 = 100 (km/h) = 100
= 100 (km/h) = 100  1000/3600 = 27.77 (m/s) となる。 これを使って、加速度を求めると
1000/3600 = 27.77 (m/s) となる。 これを使って、加速度を求めると
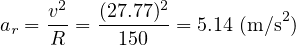
となる。