多くの場合、測定値は平均値mのまわりにつりがね形の正規分布と呼ばれる分布をする。 つまり、測定値はガウスの誤差分布関数

物理学I(授業内容:力学)
1 物理学とは
人間は自然環境の中で道具を使って社会的な生活を送る生物である。昔から人類は、天体の運行を調べて暦を作ったり、いろいろな道具を使ってきた。自然に対するこのような知的好奇心から生まれたのが物理学(physics)である。フィジックスの語源はギリシャ語で「自然の物事 natural things」を意味するフィジカで、自然科学一般を意味する。 物理学の研究の進展によって、日常生活で経験する熱現象や電磁気現象、物質の性質などの、目に見え、手で触れられる世界の法則を本当に理解するには、原子・分子の世界という直接目に見えず、手にも触れられない小さな世界のことを知らねばならないことが明らかになった。 このためには原子の構造と原子の世界を支配する量子力学の理解が必要である。
物理学の発展の歴史を振り返ると、実験結果や観察結果を速度、加速度、質量、仕事、エネルギー、温度、電荷、電流、電場、磁場、....などの物理量を導入して考察し、これらの物理量の関係(物理法則)を発見するという歴史であった。 従って、物理学を理解するには物理量とそれらが従う法則を具体的な現象や実験と関連づけて学ぶのが基本である。 物理学には「・・・法則」と呼ばれる法則が数多くあるが、これらのほとんどは適用範囲が限られている近似的な法則であることに注意する必要がある。 例えば、ニュートンの運動法則は原子の世界には適用できない。 また、電流と電圧は比例するというオームの法則があるが、ダイオードではこの法則は当てはまらない。なぜなら、金属や合金ではオームの法則に従うが、比例定数の抵抗率は物質によって異なり、温度と共に変化する。 このように、ほとんどの法則には適用できる対象と適用できない対象があり、条件が異なれば異なる値をとる定数を含む法則が多い。
(1)力学
物理学の研究では、仮説を立てて、それから導かれる結論の正否を実験で調べる研究方法が重要である。このことを最初に示したのはガリレオである。彼は、斜面を落下する物体は等加速度運動を行うことを実験と推論によって示した。
物理学では、複雑な現象そのものに正面から取り組まず、複雑な現象に寄与する色々な要因のうち、摩擦や空気の抵抗などをひとまず無視して、複雑な現象を簡素化し、簡素化された現象の研究を通じて自然の基本法則を発見しようとする方法をとっている。
ニュートンは運動の法則と万有引力の法則に基づいて、天体の運行を正確に説明し、予言できることを示した。 運動の法則と力の法則に基づいて物体の運動を研究する学問を力学という。
運動の法則は加速度という位置座標の2次導関数を含む微分方程式で表わされる。この微分形の法則を積分して導かれる法則がエネルギー保存則と運動量保存則である。
(2)熱学
蒸気機関車の発達に伴って「同じ量の燃料からどのくらい多くの動力が得られるのだろうか」というカルノーの疑問から始まったのが熱学である。
熱学の研究を通じて、全ての自然現象に共通の法則がエネルギー保存則(熱力学第一法則)と熱に関係する現象の進む方向を決めるエントロピー増大の原理(熱力学第二法則)が発見された。
(3)電磁気学
電磁気学では電荷や電流の間に力が直接に作用するのでなく、電荷や電流はその周囲に作る電場や磁場を通して他の電荷や電流に電気力や磁気力を作用していると考える。電磁気学は、電荷と電流によってどの周囲にどのような電場と磁場を作り、電場と磁場はどのように関連しているのかを研究する学問である。
電磁気学の基本法則はマクスウェル方程式で表わされる。
(4)現代物理学
19世紀末までに発達した力学、熱学、電磁気学などを古典物理学という。新しい物理学の立場から見ると、古典物理学は、研究の対象が巨視的な物質で、しかも、その速さが光の速さに比べて十分に遅い場合にのみ成り立つ。
相対性理論の誕生によって、光速に近い速さの運動法則が解明され、時間と空間の関連、質量とエネルギーの関連などが明らかにされ、原子力利用への道が開かれた。 原子の世界を支配する理論が量子論である。
量子論の誕生に引き続いて、原子、原子核、素粒子物理学などの研究が始められた。 また、物質が原子、分子の集合であるという立場から、量子論的に研究されるようになった。これが物性物理学である。
その他、生物物理学、宇宙物理学の研究も進められている。
(5)国際単位系(テキスト8ページ表0.1参照)
長さの単位としてメートル(m)、質量の単位としてキログラム(kg)、時間の単位として秒(s)をとり、これらをMKS単位系と呼ぶ。また、電流の単位のアンペア(A)を加えた単位系をMKSA単位系という。
国際単位系はMKSA単位系に温度の単位のケルビン(K)、光度の単位のカンデラ(cd)、物質量の単位のモル(mol)を加えた基本単位として構成されている。
(6)有効数字
多くの場合、測定値は平均値mのまわりにつりがね形の正規分布と呼ばれる分布をする。 つまり、測定値はガウスの誤差分布関数
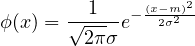
の形をとり、この関数系に従う誤差分布を正規分布という。 係数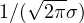 は
は を満たすように決定されている。 この分布関数を-σからσまで積分すると
を満たすように決定されている。 この分布関数を-σからσまで積分すると

となる。(テキスト9ページ図0.12参照)ここで、mは最確値(平均値)を表す。

σ(シグマ、ギリシャ文字の読みはテキスト裏表紙参照)をこの物理量の測定結果の標準偏差という。 上式の積分式はm - σとm + σの間に測定値が全体の68.3%の中に存在することを示す。
また、同様に まで積分するとS=95.4%となり、
まで積分するとS=95.4%となり、 まで積分するとS=99.7%となる。
このことは、それぞれの測定値が95.4%と99.7%の中に存在することを示す。 長さや大きさなどの物理量を測定する場合、その測定結果を
まで積分するとS=99.7%となる。
このことは、それぞれの測定値が95.4%と99.7%の中に存在することを示す。 長さや大きさなどの物理量を測定する場合、その測定結果を と表し、σを誤差という。
ある人の身長の測定値の平均値が161.414cm、標準偏差(誤差)が0.1cmの場合には、身長の測定結果の平均値として意味があるのは、161.4cm(161.4
と表し、σを誤差という。
ある人の身長の測定値の平均値が161.414cm、標準偏差(誤差)が0.1cmの場合には、身長の測定結果の平均値として意味があるのは、161.4cm(161.4 0.1cm)である。
小数点第一位の4の値に誤差が含まれているから、その桁より下の値14は必要ない。 この場合の意味ある4桁の数字の1614を有効数字という。 下記の例題でσの求め方を示す。
0.1cm)である。
小数点第一位の4の値に誤差が含まれているから、その桁より下の値14は必要ない。 この場合の意味ある4桁の数字の1614を有効数字という。 下記の例題でσの求め方を示す。
<例題>
ある物体の長さlを測って以下の値を得た。 長さの最確値(平均値)lおよび最確値の二乗平均誤差(標準偏差)σlを求めよ。
| l [cm] | δi = l -l | δi2 | |
| 1 | 143.5 | -0.11 | 1.2 ×10-2 |
| 2 | 144.2 | 0.59 | 34.8 ×10-2 |
| 3 | 143.7 | 0.09 | 0.8 ×10-2 |
| 4 | 143.6 | -0.01 | 0.0 ×10-2 |
| 5 | 143.4 | -0.21 | 4.4 ×10-2 |
| 6 | 143.5 | -0.11 | 1.2 ×10-2 |
| 7 | 143.6 | -0.01 | 0.0 ×10-2 |
| 8 | 143.3 | -0.31 | 9.6 ×10-2 |
| 9 | 143.5 | -0.11 | 1.2 ×10-2 |
| 10 | 143.8 | 0.19 | 3.6 ×10-2 |
| l = | 143.61 | ∑ δi2 = 0.568 | |
表の最後の行は、lの10回の測定値を合計してn =10で割って求めた平均値lであり、∑ δi2(δ、デルタ)は右欄の合計値である。 右欄のδi2値は測定値から平均値を引いた差δiを求め、それを二乗したものである。 平均値からのばらつきを求めるのにδiをそのまま足すと、当然0になる。 最確値の二乗平均誤差(誤差)σlは下記のように計算できる。 nは測定数を表し、例題ではn = 10である。

よって
![l = 143.610.08 [cm] = 143.61(8) [cm ]](text10x.png)
と求められる。 ここで注意すべき点は誤差 0.08[cm]の中に入っていない測定値(例えば、144.2[cm]や143.7[cm]は143.61+0.08[cm]より大きい)が数多くあることである。
「143.61
0.08[cm]の中に入っていない測定値(例えば、144.2[cm]や143.7[cm]は143.61+0.08[cm]より大きい)が数多くあることである。
「143.61  0.08[cm]」の意味するところは、測定された68.3%の測定値が
0.08[cm]」の意味するところは、測定された68.3%の測定値が  0.08[cm]の領域に入っていて、それ以外の31.7%の測定値がはみ出していることを示す。
0.08[cm]の領域に入っていて、それ以外の31.7%の測定値がはみ出していることを示す。
 まで考えた場合(例題の場合は
まで考えた場合(例題の場合は を考えた場合)、測定値の99.7%(ほぼ全て)が
を考えた場合)、測定値の99.7%(ほぼ全て)が の領域(143.61
の領域(143.61 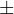 0.24[cm]の領域)に入っている。
例題では、144.2[cm]がこの領域(
0.24[cm]の領域)に入っている。
例題では、144.2[cm]がこの領域( 0.24[cm])からはみ出している。 つまり、正規分布にしたがう測定値のばらつきは、求めた誤差σの3倍程度を有する。
0.24[cm])からはみ出している。 つまり、正規分布にしたがう測定値のばらつきは、求めた誤差σの3倍程度を有する。
真値Xに関する二乗平均誤差σは各測定誤差(測定値と真値との差)ξi = xi - Xの二乗した値を合計し、測定回数nで割って平均値を求めて、その値の平方根をとったもので

で定義される。 xiは測定値で、この式と上式を比較すると(n- 1)が含まれていないことが分かる。n個が合計されているので、nで割ることは1回測定当たりの真値と測定値間の差の二乗平均値が得られる。 この値の平方根(二乗しているので平方根をとると元に戻る)が計算されることで、真値と測定値間の差の平均値が求まる。これが定義となる。 ξは3種類(クシー、クサイ、グザイ)の読み方がある。 ただし、真値のσは真値Xから計算されるものであり、真値が分からないためσは計算できない。 実際に得ることができるのは最確値(平均値)Xmであり、上式のσの定義式から最確値(平均値)の二乗平均誤差σm(例題で使用した式)を誤差の伝搬を用いて求めることができる。真値Xを使う式から、平均値Xmを使う式へ変形すると(n-1)が定義式へ加えられる。 このσmの式の求め方はHPの物理実験III、IVの最小二乗法を参照して下さい。
<例題>
円柱の直径が で、高さが
で、高さが で表されるとき、円柱の体積の最確値V = π(d∕2)2hの平均誤差σV を求めよ。誤差の伝播による最確値の誤差を求めるため、下記のようにまず偏微分
で表されるとき、円柱の体積の最確値V = π(d∕2)2hの平均誤差σV を求めよ。誤差の伝播による最確値の誤差を求めるため、下記のようにまず偏微分

を行う。 偏微分 [∂] は読み方「ラウンド」であり、微分する変数以外の変数を定数とみなして微分することを示す。 V (d,h)はdとhの変数を持ち、2変数以上を含む関数を微分する場合は微分記号「d」の代わりに偏微分記号「∂」を使う。
例えば、f(x,y) = 100x + yをxとyで偏微分すると

となる。なぜ微分が必要かというと、xが微小変化(誤差)したときに、fの変化は関数の傾き(微係数の大きさ)に依存する。 xが 1、yも
1、yも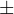 1の誤差を持つ場合、xの及ぼす誤差は
1の誤差を持つ場合、xの及ぼす誤差は となり、yより100倍の誤差がfに伝播される。
となり、yより100倍の誤差がfに伝播される。
そこで、体積の誤差σV は

と求められる。 誤差の伝播の式の求め方はHPの物理実験III、IVの最小二乗法を参照して下さい。
(7)医療最前線の物理(参考)
(a)X線診断
ターゲットに電子線を当て、X線(電磁波)を発生させて利用、造影剤を使用する場合もある。最先端の検出器として、イメージングプレート(富士フィルム開発)上の濃淡をレーザで読み取ってデジタル処理を行って利用や、フラット・パネル・イメージャ(ガラス基板上にシリコンを蒸着して半導体素子のフォトダイオードを作成)を利用する。
(b)CT(コンピュータ・トモグラフィー)診断
X線とコンピュータを用いて身体の輪切りの画像(断層像)を撮影する装置(X線管と検出器が被験者の周りを高速回転しながら、データを収集)。体の中の部位のX線吸収係数の違いを利用、0.1%程度の違いを検出(人体組織(内臓や筋肉など)の吸収係数の差は10%以内)
(c)MRI装置
H原子の核スピン(小さい磁石)の緩和時間(元の状態に戻るまでの時間)を測定して、その時間の違いを画像に表示している。
(d)シンチグラフィー、SPECT、PET診断
放射性同位元素(RI)を用いた検査法で、放射性同位元素が集まった部分について、シンチグラフィーは平面として示し、SPECTはCTやMRIのように断面画像として表示する。PETも断面画像として表示するが利用する放射線の種類が異なる。
(e)エコー(超音波)診断、超音波治療
境界面での超音波の反射を観測する。圧電素子(圧力が加わると電位が生じ、電位を加えると振動が生じる素子)を使用する。集束超音波が治療標的組織に吸収されて生じる熱によって、超音波焦域内の組織を加熱凝固することによって治療を行う。
(f)放射線治療
X線、ガンマー線、電子線を患部に照射。DNAを破壊して、細胞分裂を阻止する。正常細胞の保護のために複数の方向から照射することが必要である。
(g)陽子線、重粒子線治療
放射線の影響を受けやすい臓器のすぐそばにあるガンは陽子線(プロトンH+)、重粒子線(炭素イオンC4+、光速の80%程度まで加速)は放射線抵抗性のガンの治療に用いられている。
原理:高速の炭素イオンビームは電子と衝突しながら(方向は変わらない、質量の違いによる)エネルギーを失い速度を落とす。ただし、高速(電子より速い)のために衝突回数は少ない。炭素イオンはエネルギーを失い生体を形成する原子のまわりの電子の速度と同じ程度になると、急激に衝突回数が増加して、生体内の細胞を壊し(電子を弾き飛ばす)ながらエネルギーを失う。
現在は全国に多くの施設が建設され、300万円程度で治療可能。陽子線治療(国立がん研究センター、筑波大学、若狭湾エネルギー、静岡県立静岡がんセンター、鹿児島メディポリス医学研究財団)、重粒子線治療(兵庫県立粒子線医療センター、放射線医学総合研究所、群馬大学、九州国際重粒子線がん治療センター)などがある。
(g)レーザーメス、ハイパーサミア(温熱療法)、衝撃波結石破砕療法
レーザーは平行性にすぐれ、単色で位相が揃っている特徴を有するため、レンズで集光すると非常に細く絞ることができる。発生する熱で組織が気化・蒸発し切開される。炭酸ガス、アルゴン、ネオジウム・ヤグレイザーなどがある。
ガン細胞を高温にして死滅させるハイバーサミア療法(体の表面に電極を付け電磁波を照射することにより、照射部位の温度(43度程度)を上昇させる、原理は電子レンジと同じ)などがある。
衝撃波結石破砕療法は衝撃波を一点に集めて、結石を破壊する方法であり、手術を行う必要ない方法である。
1.1 ベクトルの基礎 – ベクトルとスカラー –
棒の「長さ」はその方向・向きに無関係な量であり、その大きさとして実数値で与えられる。時間、温度なども同様である。
従って、ベクトルは方向・向きを持つ量である。
(例えば、結晶にかかる応力 T とその結果生じる歪み S を結びつける量 S=s T、テンソルsは3×3の行列で表される。豆腐に一軸方向の力(両手で力を加えて押す)と、力が加わっている方向は縮み、力が加わっていない方向は膨れる。このような力が加わっていない方向の歪みを表すには行列で表されるテンソルsが必要となる。)
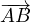 などが用いられる。
などが用いられる。
A/A で示される、大きさが 1 で方向と向きを示す場合は単位ベクトル (unit vector) という。
1.2 ベクトル代数(定義)
C=A+B、 C=A–B=A+(–B)
図に示されているように、ベクトル C は、A と B(–B)を辺とする平行 4 辺形の対角線に相当する。
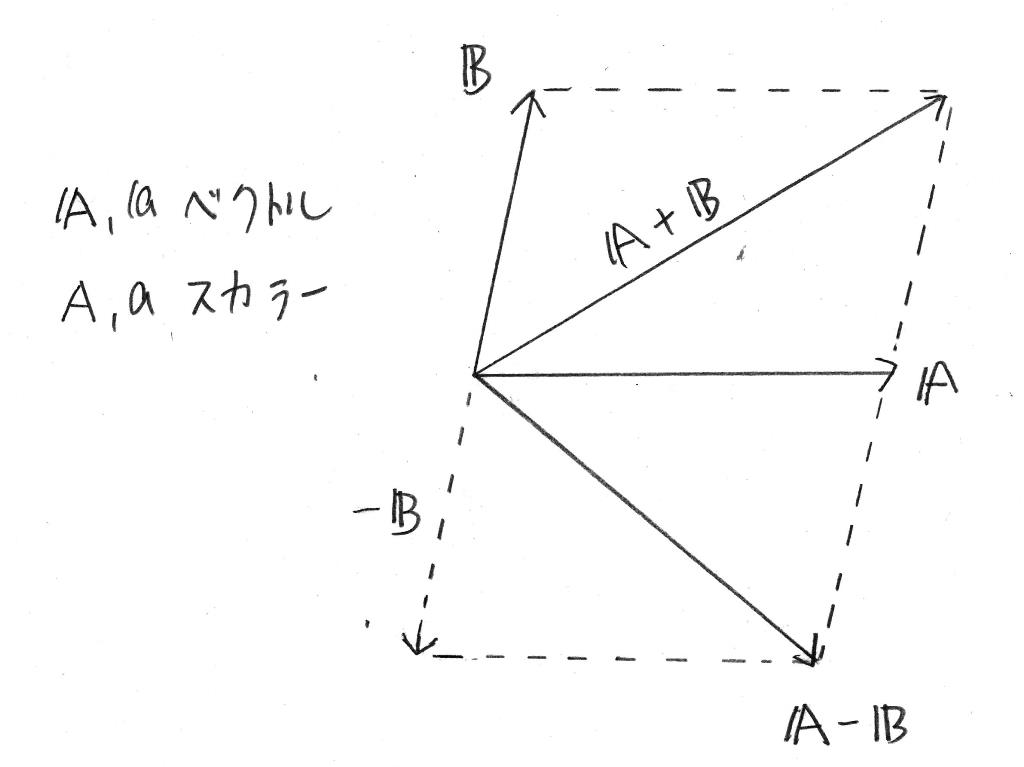
1.3 ベクトル和の幾何学的関係
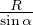 =
=  =
= 

1.4 ベクトルの成分

となる。

1.5 ベクトルの内積(スカラー積)
ベクトルの内積(スカラー積)は2つのベクトルのなす角θを使って

と定義される。また、A、B が共に微分可能ならば

となる。 2次元において、ベクトルの成分で書くと

となる。 また、図のようにベクトルA、Bのxとy方向の成分

を使って、下記のように上式を変形すると


θを使った式と同じになることが分かる。3次元において、ベクトルの成分で書くと

となる。 直交していれば、θ = 90∘ であるので cosθ = 0であり、A⋅B = 0 となる。(直交条件)また、スカラー積の分配則は下記のようになる。

また、直交系の単位ベクトル(i, j, k)は下記のように計算できる。
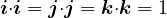


三角関数の加法定理は下記の行列式

から、


を得ることができる。
1.6 ベクトルの外積(ベクトル積) (テキストp343参照)
ベクトル A と B のベクトル積(A × B)を以下のように定義する。ただし、ベクトルの方向は右手系(直交座標系x、y、zを例に挙げると、x → y向きにネジを回すとき進む向きがz方向になる系)で考える。 A × Bは大きさ AB sinθ(平行四辺形の面積)であり、A と B によって作られる面に垂直な方向(A と Bの両方に垂直な方向)を有するベクトルである。

![(A × [B + C ]) = A × B +A ×C](text47x.png)


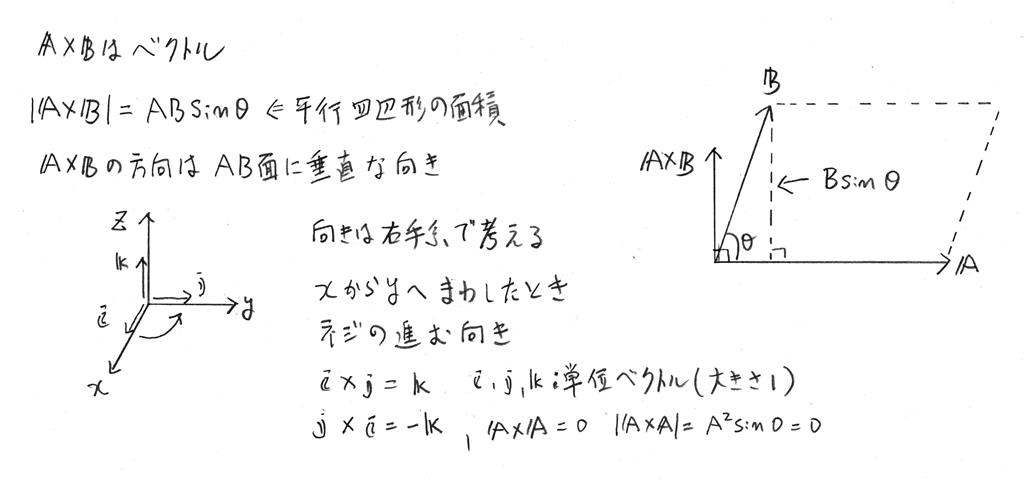
ここで、i、j、kは単位ベクトルである。ベクトルAとBの成分を下記のように3次元で表して

AとBのベクトル積を計算すると、下記のように成分ごとに計算され、方向は上式の単位ベクトルの方向によって決まる。

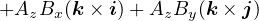

の関係式を使用して、ベクトル表示で表すと

となる。また、得られたA×Bを成分表示にすると

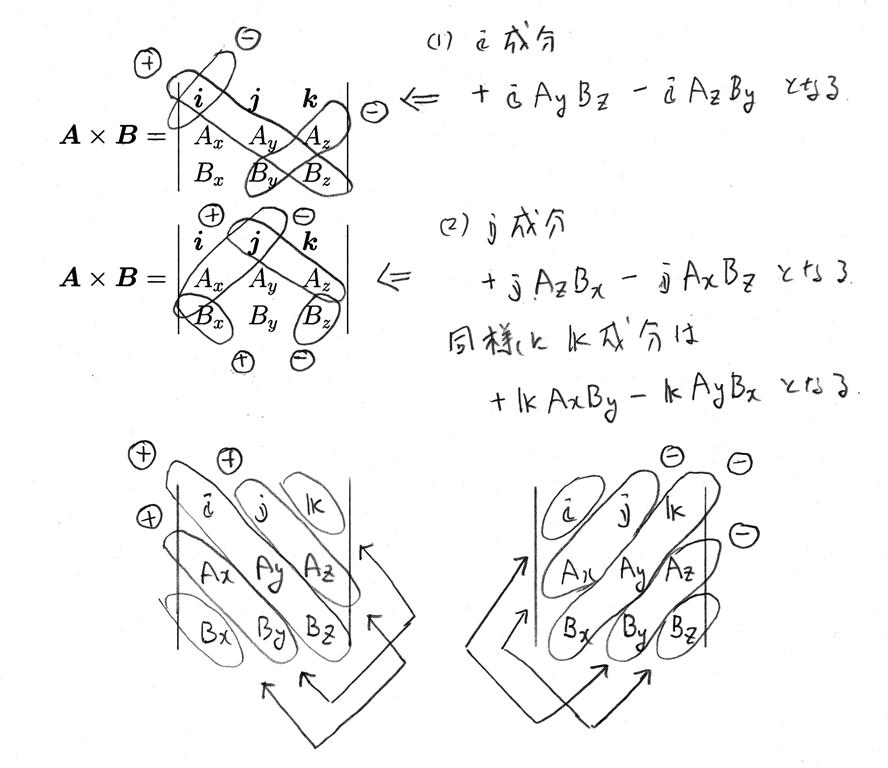
と書ける。 また、行列表示でA×Bを書くと

となる。ベクトル積の成分を求めるにはこの行列式を使って求める方が簡単である。 図のように、i成分は右下方向のi、Ay、Bz成分を掛け、左下方向のi、Az、Byを掛けて負にする。jとk成分も同様にして求めると

が得られる。